こんにちは、数学講師の山本敦子です。今日は、グラフのスケールについてのお話です。

去年の今頃、感染が広がるコロナに関して、数学科の友人たちとやりとりをしていました。日本、オランダ、アメリカ、など、それぞれの国の情報交換をしていたところ、こんな表が見られるサイトを見つけました。

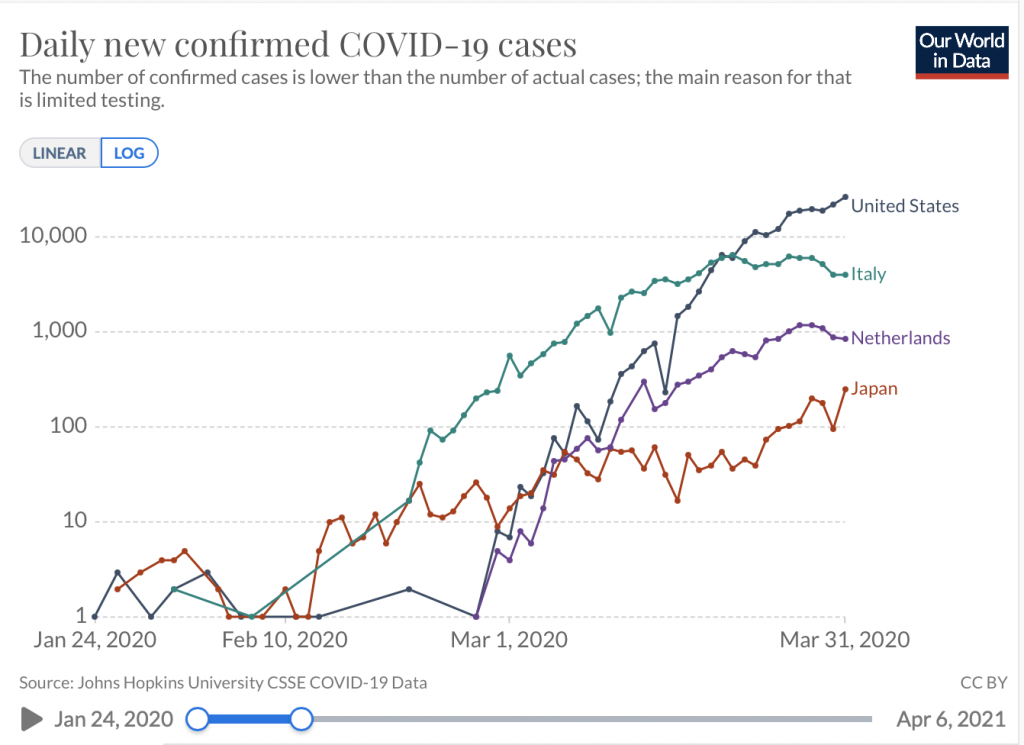
これはその時に見た 2020年の3月31日までの国ごとの新規感染者のグラフです。「イタリアでの感染の広がりが大変だったけど、今ではアメリカだね。」「ほんとだ。ぐんぐん伸びているね。」「日本も上向きだね。」「感染は油断すると指数関数的に増えちゃうから、横ばいでも、直線でもありがたいんだって。」「あ、ここはクイっと上向きになって、指数関数的になっちゃうんじゃないかと心配だね。」と意見を交わしているその時に気付きました。「ちょっとちょっと、これ、片対数グラフだよ！（ってことは、右上がりの直線で指数関数なんだ、、、、）」（絶句）

片対数グラフというのは、$x$ 軸、$y$ 軸のどちらかが対数スケールになっているグラフで、例えば、
$x$ 軸（横軸）は等間隔で $0$, $1$, $2$, $3$, $4$, … を表し、
$y$ 軸（縦軸）は等間隔で $10^0$, $10^1$, $10^2$, $10^3$, … を表したものです。

上のグラフが片対数グラフであることは縦軸のメモリが $1$, $10$, $100$, $1000$, $10000$ であることからわかりますね。
$$(1=10^0,\qquad 10=10^1,\qquad 100=10^2,\qquad 1000=10^3,\qquad10000=10^4)$$

どうして、片対数グラフを使っているのでしょうか。それは、感染が指数関数的に増えてしまっていたからなんです。

$y$ が $x$ の指数関数であるとは、
$$y=a^x$$
$(a>0 かつ a\not= 0)$ と表せるということです。（正しくいうと、この時 $y$ は $a$ を底とする $x$ の指数関数である、という。）

話を単純にして、患者一人から、１週間後に５人に感染するとする。 （2週目以降にはもう感染させないとしておきましょう。）最初に患者が一人いると、１週間後の新規感染者は５人になる。その５人がそれぞれ１週間後に５人に感染させると、２週間後の新規感染者は $5\times 5 =5^2$人（$=25$ 人）になる。この$5^2$ 人の新規感染者が、その１週間後に 5 人に感染させるので、3 週間後の新規感染者は $5^2 \times 5=5^3$ 人（=$125$ 人）。4週間後には $5^3 \times 5=5^4$ 人（$=625$ 人）つまり $x$ 週間後の（前の週の新規感染者から感染した）新規感染者は
$$y=5^x$$
となり、指数関数となっているわけです。指数関数は、底が $1$ より大きい時には、増加の仕方がどんどん激しくなります。これがコロナの感染の広がりを心配する理由です。

グラフで見てみましょう。
・青い線が 1 人が ２ 人に感染させるモデル。式は　$y=2^x$
・赤い線が 1 人が ５ 人に感染させるモデル。式は　$y=5^x$
で、$x$ 週間目にどのような数になるのか。通常のスケールのグラフではこのようになります。　

すぐに上に消えてしまい、５週間後からは範囲外です。縦軸の数をものすごく大きな数にしないと視界に入ってきません。

これが、片対数グラフになると、次ようになります。

どちらも画面の中に収まりました。ただし、読み取る時には、縦軸の幅が上に行くほど大きな差を示していることを忘れてはいけません。

では、最初に見た、2020年3月までのコロナ陽性判定の人数のグラフを通常のスケールでみてみましょう。

左上のスイッチを "linear" に切り替えて、縦軸のメモリが、$5000$, $10,000$, $15,000$ となっていて、通常の線形グラフであることがわかります。このグラフでは、アメリカがダントツで、他をどのくらい引き離して多くなっているのかがとてもよくわかりますね。ただし、その大きな数を入れるために、小さな数での上げ下げや差が潰れてしまい、見にくくなり、日本の上下などわからなくなってしまっています。片対数グラフでは、数が小さいときも、ものすごく大きくになったときにも、それぞれの数の周りでの比較がしやすかったんだなあと気付きます。

見比べたい人のために、片対数グラフと、線形グラフを隣に並べてみます。同じデータからできたグラフとは思えませんね。印象がかなり違います。何を知りたいかにより、どちらが便利かがちがってきますね。

片対数グラフ

通常のグラフ（線形グラフ）

数学はいつもとなりに。

ここで紹介したグラフのサイト：Our World in Data
https://ourworldindata.org/explorers/coronavirus-data-explorer?yScale=log&zoomToSelection=true&time=earliest..70&pickerSort=asc&pickerMetric=location&Metric=Confirmed+cases&Interval=New+per+day&Relative+to+Population=false&Align+outbreaks=false&country=USA~ITA~NLD~JPN